一、三角形面积公式概述

在数学学习中，三角形是基础几何图形之一。三角形面积的计算是几何学中的基本技能。常见的三角形面积公式主要有两种：一是底乘以高除以二，二是使用海伦公式计算。了解和熟练掌握这些公式是解决三角形面积问题的关键。

二、基本三角形面积计算

1. 直角三角形面积计算

直角三角形是最常见的三角形，其面积计算相对简单。对于直角三角形，面积可以通过直角边长直接计算，公式为：面积 = 底 × 高 ÷ 2。例如，如果一个直角三角形的两条直角边长分别为3cm和4cm，那么其面积就是 3cm × 4cm ÷ 2 = 6cm²。

2. 等腰三角形面积计算

等腰三角形有一边等于底边，其他两边相等。等腰三角形的面积可以通过底边和高来计算，公式与直角三角形相同。例如，如果一个等腰三角形的底边长为6cm，高为4cm，那么其面积就是 6cm × 4cm ÷ 2 = 12cm²。

3. 普通三角形面积计算

对于普通的三角形，我们可以使用海伦公式来计算面积。海伦公式是：面积 = √(s × (s - a) × (s - b) × (s - c))，其中s是半周长，a、b、c是三角形的三边长。例如，如果一个三角形的三边长分别为3cm、4cm和5cm，那么半周长s = (3 + 4 + 5) ÷ 2 = 6cm，面积 = √(6 × (6 - 3) × (6 - 4) × (6 - 5)) = √(6 × 3 × 2 × 1) = √36 = 6cm²。

三、特殊三角形面积计算

1. 等边三角形面积计算

等边三角形的三边都相等，其面积可以通过边长直接计算。公式为：面积 = (边长 × 边长 × √3) ÷ 4。例如，如果一个等边三角形的边长为6cm，那么其面积就是 (6cm × 6cm × √3) ÷ 4 = 9√3 cm²。

2. 高度为0的三角形面积计算

当三角形的高为0时，实际上是一个退化三角形，其面积也为0。这种情况在理论上存在，但在实际应用中很少遇到。

四、三角形面积问题解题技巧

1. 分析题目类型

在解决三角形面积问题时，首先要分析题目类型，确定使用哪种公式。例如，如果是直角三角形，就使用底乘以高除以二的公式；如果是普通三角形，就使用海伦公式。

2. 找到关键数据

在解题过程中，要仔细阅读题目，找到关键数据。例如，题目中给出的三边长、角度、高或者周长等，都是计算面积所必需的。

3. 绘制图形

对于复杂的问题，绘制图形可以帮助我们更好地理解题意，找到解题思路。特别是在解决与三角形相关的几何问题时，图形是非常有用的工具。

4. 检验答案

在得到答案后，要仔细检查计算过程和结果。可以通过代入原始数据验证答案的正确性，确保没有计算错误。

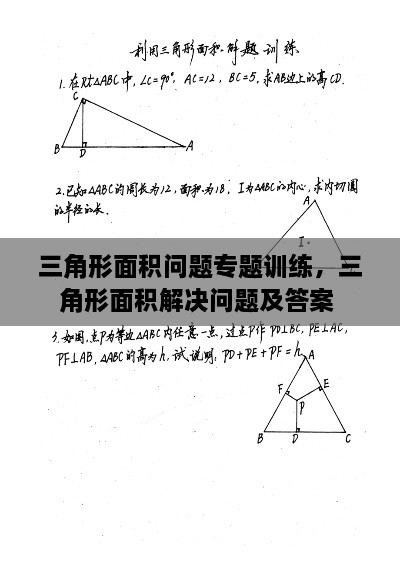
五、三角形面积问题专题训练案例

案例一：已知一个三角形的底边长为8cm，高为6cm，求该三角形的面积。

解答：根据公式面积 = 底 × 高 ÷ 2，代入数据得面积 = 8cm × 6cm ÷ 2 = 24cm²。

案例二：已知一个三角形的三边长分别为5cm、12cm和13cm，求该三角形的面积。

解答：首先计算半周长s = (5 + 12 + 13) ÷ 2 = 15cm，然后使用海伦公式计算面积：面积 = √(15 × (15 - 5) × (15 - 12) × (15 - 13)) = √(15 × 10 × 3 × 2) = √900 = 30cm²。

通过